9.4. Funkcje w mcpi¶
O Minecrafcie w wersji na Raspberry Pi myśleć można jak o atrakcyjnej formie wizualizacji tego co można przedstawić w grafice dwu- lub trójwymiarowej. Zobaczmy zatem jakie budowle otrzymamy, wyliczając współrzędne bloków za pomocą funkcji matematycznych. Przy okazji niejako przypomnimy sobie użycie opisywanej już w naszych scenariuszach biblioteki matplotlib, która jest dedykowanym dla Pythona środowiskiem tworzenia wykresów 2D.
9.4.1. Funkcja liniowa¶
Za pomocą wybranego edytora utwórz pusty plik, umieść w nim podany niżej kod i zapisz
w katalogu mcpi-sim pod nazwą mcpi-funkcje.py:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 | #!/usr/bin/env python
# -*- coding: utf-8 -*-
import os
import numpy as np # import biblioteki do obliczeń naukowych
import matplotlib.pyplot as plt # import biblioteki do tworzenia wykresów
import mcpi.minecraft as minecraft # import modułu minecraft
import mcpi.block as block # import modułu block
os.environ["USERNAME"] = "Steve" # wpisz dowolną nazwę użytkownika
os.environ["COMPUTERNAME"] = "mykomp" # wpisz dowolną nazwę komputera
mc = minecraft.Minecraft.create("192.168.1.10") # połaczenie z mc
def plac(x, y, z, roz=10, gracz=False):
"""
Funkcja tworzy podłoże i wypełnia sześcienny obszar od podanej pozycji,
opcjonalnie umieszcza gracza w środku.
Parametry: x, y, z - współrzędne pozycji początkowej,
roz - rozmiar wypełnianej przestrzeni,
gracz - czy umieścić gracza w środku
Wymaga: globalnych obiektów mc i block.
"""
podloga = block.STONE
wypelniacz = block.AIR
# podloga i czyszczenie
mc.setBlocks(x, y - 1, z, x + roz, y - 1, z + roz, podloga)
mc.setBlocks(x, y, z, x + roz, y + roz, z + roz, wypelniacz)
# umieść gracza w środku
if gracz:
mc.player.setPos(x + roz / 2, y + roz / 2, z + roz / 2)
def wykres(x, y, tytul="Wykres funkcji", *extra):
"""
Funkcja wizualizuje wykres funkcji, której argumenty zawiera lista x
a wartości lista y i ew. dodatkowe listy w parametrze *extra
"""
if len(extra):
plt.plot(x, y, extra[0], extra[1]) # dwa wykresy na raz
else:
plt.plot(x, y)
plt.title(tytul)
# plt.xlabel(podpis)
plt.grid(True)
plt.show()
def fun1(blok=block.IRON_BLOCK):
"""
Funkcja f(x) = a*x + b
"""
a = int(raw_input('Podaj współczynnik a: '))
b = int(raw_input('Podaj współczynnik b: '))
x = range(-10, 11) # lista argumentów x = <-10;10> z krokiem 1
y = [a * i + b for i in x] # wyrażenie listowe
print x, "\n", y
wykres(x, y, "f(x) = a*x + b")
for i in range(len(x)):
mc.setBlock(x[i], 1, y[i], blok)
def main():
mc.postToChat("Funkcje w Minecrafcie") # wysłanie komunikatu do mc
plac(-80, 0, -80, 160)
mc.player.setPos(22, 10, 10)
fun1()
return 0
if __name__ == '__main__':
main()
|
Większość kodu powinna być już zrozumiała, czyli importy bibliotek, nawiązywania połączenia
z serwerem MC Pi, czy funkcja plac() tworząca przestrzeń do testów.
Podobnie funkcja wykres(), która pokazuje nam graficzną reprezentację funkcji
za pomocą biblioteki matblotlib. Na uwagę zasługuje w niej tylko parametr *extra,
który pozwala przekazać argumenty i wartości dodatkowej funkcji.
Funkcja fun1() pobiera od użytkownika dwa współczynniki i odwzorowuje argumenty
z dziedziny <-10;10> na wartości wg liniowego równania: f(x) = a * x + b.
Przeciwdziedzinę można byłoby uzyskać “na piechotę” za pomocą kodu:
y = []
for i in x:
y.append(a * i + b)
– ale efektywniejsze jest wyrażenie listowe: y = [a * i + b for i in x].
Po zobrazowaniu wykresu za pomocą funkcji funkcji wykres() i biblioteki matplotlib
“budujemy” ją w MC Pi w pętli odczytującej wyliczone pary argumentów i wartości funkcji,
stanowiących współrzędne kolejnych bloków umieszczanych poziomo.
Uruchom i przetestuj omówiony kod podając współczynniki np. 4 i 6.
9.4.2. Układ współrzędnych¶
Spróbujmy pokazać w Mc Pi układ współrzędnych oraz ułatwić “budowanie” wykresów
za pomocą osobnej funkcji. Po funkcji wykres() umieszczamy w pliku mcpi-funkcje.py nowy kod:
52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 | def uklad(blok=block.OBSIDIAN):
"""
Funkcja rysuje układ współrzędnych
"""
for i in range(-80, 81, 2):
mc.setBlock(i, -1, 0, blok)
mc.setBlock(0, -1, i, blok)
mc.setBlock(0, i, 0, blok)
def rysuj(x, y, z, blok=block.IRON_BLOCK):
"""
Funkcja wizualizuje wykres funkcji, umieszczając bloki w pionie/poziomie
w punktach wyznaczonych przez pary elementów list x, y lub x, z
"""
czylista = True if len(y) > 1 else False
for i in range(len(x)):
if czylista:
print(x[i], y[i])
mc.setBlock(x[i], y[i], z[0], blok)
else:
print(x[i], z[i])
mc.setBlock(x[i], y[0], z[i], blok)
|
– a pętlę tworzącą wykres w funkcji fun1() zastępujemy wywołaniem:
rysuj(x, y, [1], blok)
Funkcja rysuj() potrafi zbudować bloki zarówno w poziomie, jak i w pionie w zależności
od tego, czy lista wartości funkcji przekazana zostanie jako parametr y czy też z.
Do rozpoznania tego wykorzystujemy zmienną sterującą ustawianą w instrukcji: czylista = True if len(y) > 1 else False.
Zawartość funkcji main() zmieniamy na:
90 91 92 93 94 95 96 | def main():
mc.postToChat("Funkcje w Minecrafcie") # wysłanie komunikatu do mc
plac(-80, -40, -80, 160)
mc.player.setPos(-4, 10, 20)
uklad()
fun1()
return 0
|
Po uruchomieniu zmienionego kodu powinniśmy zobaczyć wykres naszej funkcji w pionie.
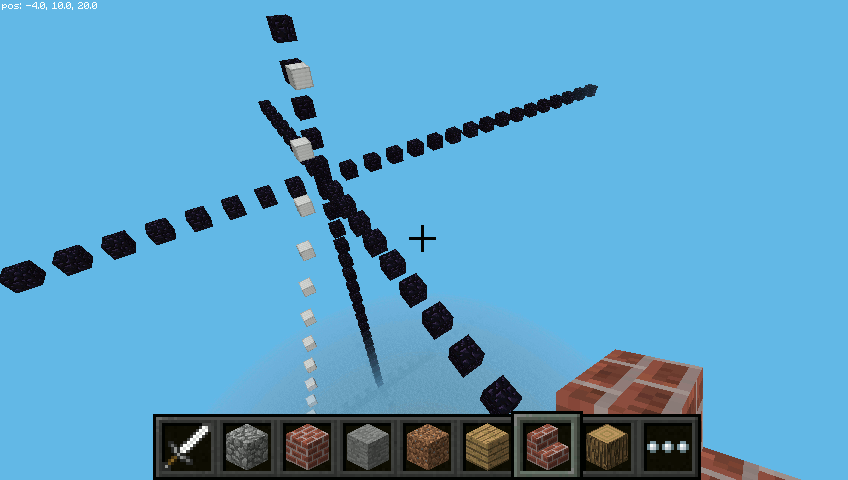
Kod “budujący” wykresy funkcji możemy urozmaicić wykorzystując poznaną wcześniej
bibliotekę minecraftstuff. Poniżej funkcji rysuj() dodajemy:
77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 | def rysuj_linie(x, y, z, blok=block.IRON_BLOCK):
"""
Funkcja wizualizuje wykres funkcji, umieszczając bloki w pionie/poziomie
w punktach wyznaczonych przez pary elementów list x, y lub x, z
przy użyciu metody drawLine()
"""
import local.minecraftstuff as mcstuff
mcfig = mcstuff.MinecraftDrawing(mc)
czylista = True if len(y) > 1 else False
for i in range(len(x) - 1):
x1 = int(x[i])
x2 = int(x[i + 1])
if czylista:
y1 = int(y[i])
y2 = int(y[i + 1])
print (x1, y1, z[0], x2, y2, z[0])
mcfig.drawLine(x1, y1, z[0], x2, y2, z[0], blok)
else:
z1 = int(z[i])
z2 = int(z[i + 1])
print (x1, y[0], z1, x2, y[0], z2)
mcfig.drawLine(x1, y[0], z1, x2, y[0], z2, blok)
|
– a wywołanie rysuj() w funkcji fun1() zmieniamy na rysuj_linie().
Sprawdź rezultat.
9.4.3. Kolejne funkcje¶
W pliku mcpi-funkcje.py tuż nad funkcją główną main() umieszczamy kod
wyliczający dziedziny i przeciwdziedziny dwóch kolejnych funkcji:
114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 | def fun2(blok=block.REDSTONE_ORE):
"""
Wykres funkcji f(x), gdzie x = <-1;2> z krokiem 0.15, przy czym
f(x) = x/(x+2) dla x >= 1
f(x) = x*x/3 dla x < 1 i x > 0
f(x) = x/(-3) dla x <= 0
"""
x = np.arange(-1, 2.15, 0.15) # lista argumentów x
y = [] # lista wartości f(x)
for i in x:
if i <= 0:
y.append(i / -3)
elif i < 1:
y.append(i ** 2 / 3)
else:
y.append(i / (i + 2))
wykres(x, y, "Funkcja mieszana")
x = [round(i * 20, 2) for i in x]
y = [round(i * 20, 2) for i in y]
print x, "\n", y
rysuj(x, y, [1], blok)
def fun3(blok=block.LAPIS_LAZULI_BLOCK):
"""
Funkcja f(x) = log2(x)
"""
x = np.arange(0.1, 41, 1) # lista argumentów x
y = [np.log2(i) for i in x]
y = [round(i, 2) * 2 for i in y]
print x, "\n", y
wykres(x, y, "Funkcja logarytmiczna")
rysuj(x, y, [1], blok)
def main():
mc.postToChat("Funkcje w Minecrafcie") # wysłanie komunikatu do mc
plac(-80, -20, -80, 160)
mc.player.setPos(-8, 10, 26)
uklad(block.DIAMOND_BLOCK)
fun1()
fun2()
fun3()
return 0
|
W funkcji fun2() wartości dziedziny uzyskujemy dzięki metodzie arange(start, stop, step) z biblioteki numpy. Potrafi ona generować listę wartości zmiennopozycyjnych w podanym zakresie <start;stop) z określonym krokiem step.
Przeciwdziedzinę wyliczamy w pętli w zależności od przedziałów, w których znajdują się argumenty,
za pomocą złożonej instrukcji warunkowej. Następnie wartości zarówno dziedziny, jak i przeciwdziedziny
przeskalowujemy w wyrażeniach listowych, mnożąc przez stały współczynnik,
aby wykres w MC Pi był większy i wyraźniejszy. Przy okazji współrzędne zaokrąglamy
do dwóch miejsc po przecinku, np.: x = [round(i * 20, 2) for i in x].
W funkcji fun3() w podobny jak powyżej sposób obliczamy argumenty i wartości funkcji logarytmicznej.
Na koniec zmieniamy też nieco wywołania w funkcji głównej. Przetestuj podany kod.
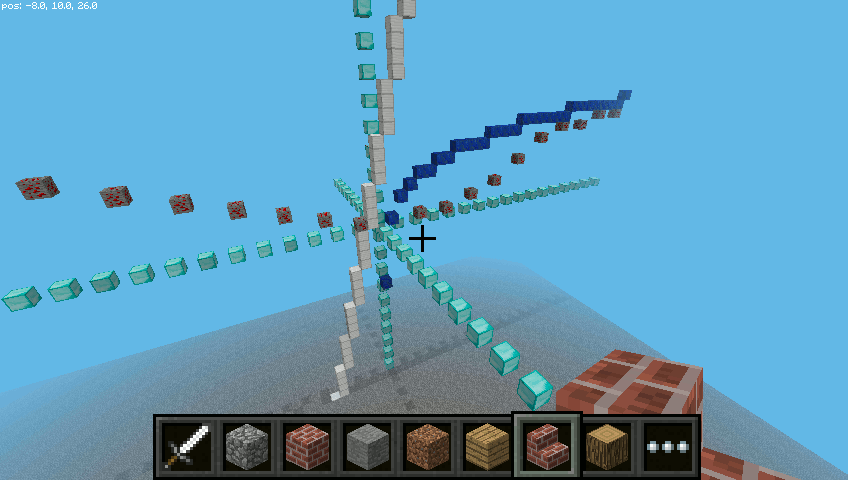
9.4.4. Funkcja kwadratowa¶
Przygotujemy wykres funkcji kwadratowej. Przed funkcją główną umieszczamy następujący kod:
150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 | def fkw(x, a=0.3, b=0.1, c=0):
return a * x**2 + b * x + c
def fkwadratowa():
"""
Funkcja przygotowuje dziedzinę funkcji kwadratowej
oraz dwie przeciwdziedziny, druga z odwróconym znakiem. Następnie
buduje ich wykresy w poziomie i w pionie.
"""
while True:
lewy = float(raw_input("Podaj lewy kraniec przedziału: "))
prawy = float(raw_input("Podaj prawy kraniec przedziału: "))
if lewy * prawy < 1 and lewy <= prawy:
break
print lewy, prawy
# x = np.arange(lewy, prawy, 0.2)
x = np.linspace(lewy, prawy, 60, True)
x = [round(i, 2) for i in x]
y1 = [fkw(i) for i in x]
y1 = [round(i, 2) for i in y1]
y2 = [-fkw(i) for i in x]
y2 = [round(i, 2) for i in y2]
print x, "\n", y1, "\n", y2
wykres(x, y1, "Funkcja kwadratowa", x, y2)
rysuj_linie(x, [1], y1, block.GRASS)
rysuj(x, [1], y2, block.SAND)
rysuj(x, y1, [1], block.WOOL)
rysuj_linie(x, y2, [1], block.IRON_BLOCK)
def main():
mc.postToChat("Funkcje w Minecrafcie") # wysłanie komunikatu do mc
plac(-80, -20, -80, 160)
mc.player.setPos(-15, 10, -15)
uklad(block.OBSIDIAN)
fkwadratowa()
return 0
|
Na początku w funkcji fkwadratowa() pobieramy od użytkownika przedział, w którym
budować będziemy funkcję. Wymuszamy przy tym w pętli while, aby lewa i prawa granica
miały inne znaki. Dalej używamy funkcji linspace(start, stop, num, endpoint), która generuje
listę num wartości od punktu początkowego do końcowego, który uwzględniany jest, jeżeli argument
endpoint ma wartość True. Kolejne wyrażenia listowe wyliczają przeciwdziedziny
i zaokrąglają wartości do 2 miejsc po przecinku.
Sama funkcja kwadratowa a*x^2 + b*x + c zdefiniowana jest w funkcji fkw(), do której
przekazujemy kolejne argumenty dziedziny i opcjonalnie współczynniki.
Instrukcje rysuj() i rysuj_linie() dzięki przekazywaniu przeciwdziedziny jako
2. lub 3. argumentu budują wykresy w poziomie lub w pionie za pomocą pojedynczych
lub połączonych bloków.
Po przygotowaniu w funkcji głównej miejsca, ustawieniu gracza, narysowaniu układu i podaniu przedziału <-20, 20> otrzymamy konstrukcję podobną do poniższej.
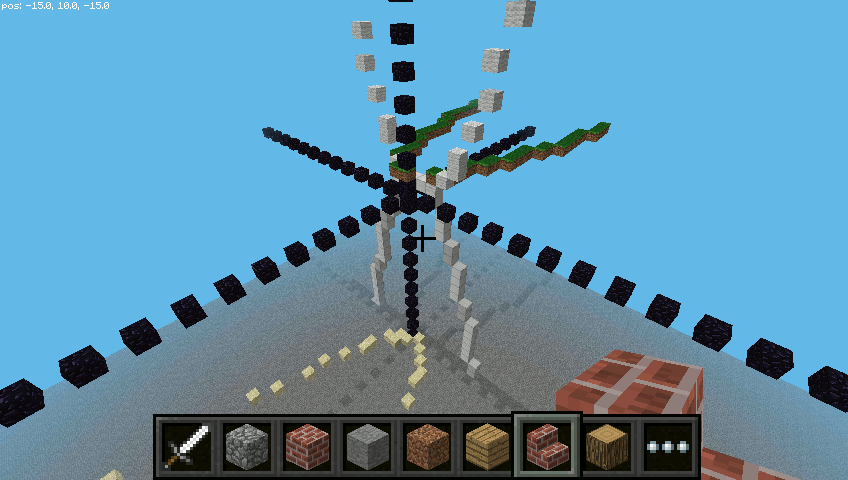
Po zmianie funkcji na x**2 / 3 można otrzymać:
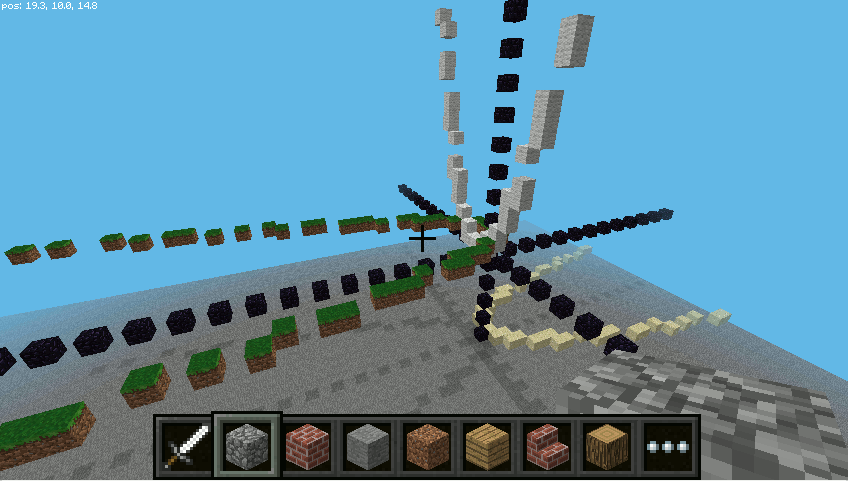
Zwróciłeś uwagę na to, że jeden z wykresów opada?
9.4.5. Funkcje trygonometryczne¶
Na koniec zobrazujemy funkcje trygonometryczne. Przed funkcją główną dopisujemy kod:
182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 | def trygon():
x1 = np.arange(-50.0, 50.0, 1)
y1 = 5 * np.sin(0.1 * np.pi * x1)
y1 = [round(i, 2) for i in y1]
print x1, "\n", y1
x2 = range(0, 361, 10) # lista argumentów x
y2 = [None if i == 90 or i == 270 else np.tan(i * np.pi / 180) for i in x2]
x2 = [i // 10 for i in x2]
y2 = [round(i * 3, 2) if i is not None else None for i in y2]
print x2, "\n", y2
wykres(x1, y1, "Funkcje sinus i tangens", x2, y2)
del x2[9] # usuń 10 element listy
del y2[9] # usuń 10 element listy
del x2[x2.index(27)] # usuń element o wartości 27
del y2[y2.index(None)] # usuń element None
print x2, "\n", y2
rysuj(x1, [1], y1, block.GOLD_BLOCK)
rysuj(x2, y2, [1], block.OBSIDIAN)
def main():
mc.postToChat("Funkcje w Minecrafcie") # wysłanie komunikatu do mc
plac(-80, -20, -80, 160)
mc.player.setPos(17, 17, 24)
uklad(block.DIAMOND_BLOCK)
trygon()
return 0
|
W funkcji trygon() na początku wyliczamy dziedzinę i przeciwdziedzinę funkcji
5 * sin(0.1 * Pi * x), przy czym wartości y zaokrąglamy.
Dalej generujemy argumenty x dla funkcji tangens w przedziale od 0 do 360 co 10 stopni.
Obliczając wartości y za pomocą wyrażenia listowego
y2 = [None if i == 90 or i == 270 else np.tan(i * np.pi / 180) for i in x2]
dla argumentów 90 i 270 wstawiamy None (czyli nic), ponieważ dla tych argumentów
funkcja nie przyjmuje wartości. Dzięki temu uzyskamy poprawny wykres w matplotlib.
Aby wykresy obydwu funkcji nałożyły się na siebie, używając wyrażenia listowego,
skalujemy argumenty i wartości funkcji tangens. Pierwsze dzielimy przez 10, drugie
mnożymy przez 3 (i przy okazji zaokrąglamy). Konstrukcja if i is not None else None
zapobiega wykonywaniu operacji dla wartości None, co generowałoby błędy.
Przygotowanie danych do zwizualizowania w Minecrafcie wymaga usunięcia 2 argumentów
z listy x2 oraz odpowiadających im wartości None z listy y2, ponieważ nie tworzą
one poprawnych współrzędnych. Pierwszą parę usuwamy podając wprost odpowiedni indeks
w instrukcjach del x2[9] i del y2[9]. Indeksy elementów drugiej pary najpierw
wyszukujemy x2.index(27) i y2.index(None), a później przekazujemy do
instrukcji usuwającej del().
Po wywołaniu z ustawieniami w funkcji głównej takimi jak w powyższym kodzie powinniśmy zobaczyć obraz podobny do poniższego.
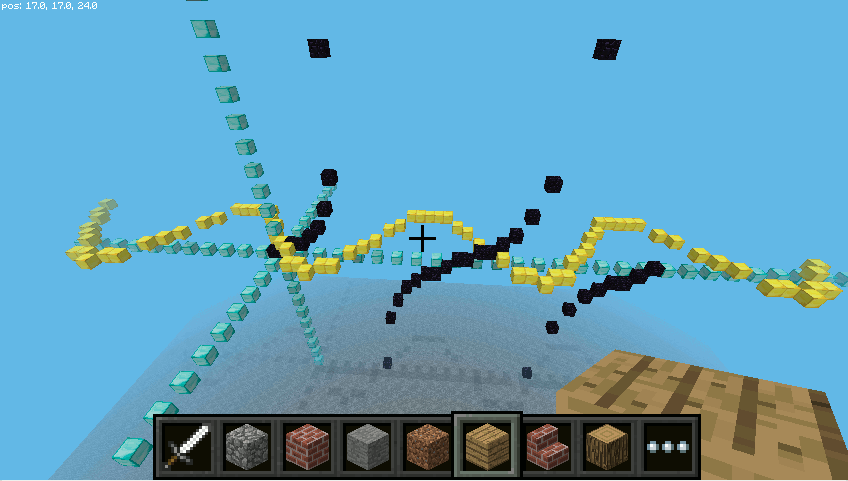
Ćwiczenia
Warto poeksperymentować z wzorami funkcji, ich współczynnikami, wartościami przedziałów i ilością argumentów, aby zbadać jak te zmiany wpływają na ich reprezentację graficzną.
Można też rysować mieszać metody rysujące wykresy (rysuj(), rysuj_linie()),
kolejność przekazywania im parametrów, rodzaje bloków itp.
Spróbuj np. budować wykresy z piasku (block.STONE) ponad powierzchnią.
Źródła:
 Materiały Python 101
udostępniane przez
Centrum Edukacji Obywatelskiej na licencji
Creative Commons Uznanie autorstwa-Na tych samych warunkach 4.0 Międzynarodowa.
Materiały Python 101
udostępniane przez
Centrum Edukacji Obywatelskiej na licencji
Creative Commons Uznanie autorstwa-Na tych samych warunkach 4.0 Międzynarodowa.
| Utworzony: | 2022-05-22 o 19:52 w Sphinx 1.5.3 |
|---|---|
| Autorzy: | Patrz plik “Autorzy” |