2. Matplotlib¶

Jedną z potężniejszych bibliotek Pythona jest matplotlib, która służy do tworzenia różnego rodzaju wykresów. Pylab to API ułatwiające korzystanie z omawianej biblioteki na wzór środowiska Matlab. Poniżej pokazujemy, jak łatwo przy użyciu Pythona wizualizować wykresy różnych funkcji.

Zobacz, jak zainstalować matplotlib w systemie Linux lub Windows.

Informacja

W systemach Linux matplotlib wymaga pakietu python-tk (systemy oparte na Debianie) lub tk (systemy oparte na Arch Linux).

Funkcja liniowa
Dwie funkcje
Ruchy Browna
Zadania dodatkowe
Źródła

Informacja

Bibliotekę matplotlib można importować na kilka sposobów. Najprostszym jest użycie instrukcji import pylab, która udostępnia moduł pyplot (do tworzenia wykresów) oraz bibliotekę numpy (funkcje matematyczne) w jednej przestrzeni nazw. Tak będziemy robić w konsoli i początkowych przykładach.

Oficjalna dokumentacja sugeruje jednak, aby w bardziej złożonych projektach stosować jawne importy podane niżej. Tak zrobimy w przykładach korzystających z funkcji matematycznych.

import numpy as np
import matplotlib.pyplot as plt

Wskazówka

Jeżeli konsolę rozszerzoną uruchomimy poleceniem ipython --pylab, nie trzeba będzie podawać przedrostka pylab przy korzystaniu z funkcji rysowania.

2.1. Funkcja liniowa ¶

Zabawę zacznijmy w konsoli Pythona:

Terminal. Kod nr

import pylab
x = [1,2,3]
y = [4,6,5]
pylab.plot(x,y)
pylab.show()

Tworzenie wykresów jest proste. Musimy mieć zbiór wartości x i odpowiadający im zbiór wartości y. Obie listy przekazujemy jako argumenty funkcji plot(), a następnie rysujemy funkcją show().

Spróbujmy zrealizować bardziej złożone zadanie.

ZADANIE: wykonaj wykres funkcji f(x) = a*x + b, gdzie x = <-10;10> z krokiem 1, a = 1, b = 2.

W pliku pylab01.py umieszczamy poniższy kod:

Kod nr

#! /usr/bin/env python3
# -*- coding: utf-8 -*-

import pylab

a = 1
b = 2
x = range(-10, 11)  # lista argumentów x

y = []  # lista wartości
for i in x:
    y.append(a * i + b)

pylab.plot(x, y)
pylab.title('Wykres f(x) = a*x - b')
pylab.grid(True)
pylab.show()

Na początku dla ułatwienia importujemy interfejs pylab. Następnie postępujemy wg omówionego schematu: zdefiniuj dziedzinę argumentów funkcji, a następnie zbiór wyliczonych wartości. W powyższym przypadku generujemy listę wartości x za pomocą funkcji range() – co warto przetestować w interaktywnej konsoli Pythona. Wartości y wyliczamy w pętli i zapisujemy w liście.

Dodatkowe metody: title() ustawia tytuł wykresu, grid() włącza wyświetlanie pomocniczej siatki. Uruchom program.

2.1.1. Ćwiczenie 1¶

Zmodyfikuj kod tak, aby współczynniki a i b mógł podawać użytkownik. Nie zapomnij przekonwertować danych tekstowych na liczby całkowite.

2.1.2. Ćwiczenie 2¶

W konsoli Pythona wydajemy następujące polecenia:

Terminal. Kod nr

>>> a = 2
>>> x = range(11)
>>> for i in x:
...   print(a + i)
>>> y = [a + i for i in range(11)]
>>> print(y)

Powyższy przykład wykorzystuje tzw. wyrażenie listowe, które zwięźle zastępuje pętlę i zwraca listę wartości. Jego działanie należy rozumieć następująco: dla każdej wartości i (nazwa zmiennej dowolna) w liście x wylicz wyrażenie a + i i umieść w liście y.

Użyj wyrażenia listowego w naszym programie:

Kod nr

a = int(input('Podaj współczynnik a: '))
b = int(input('Podaj współczynnik b: '))
x = range(-10, 11)  # lista argumentów x

# wyrażenie listowe wylicza dziedzinę y
y = [a * i + b for i in x]  # lista wartości

2.2. Dwie funkcje ¶

ZADANIE: wykonaj wykres funkcji:

f(x) = x/(-3) + a dla x <= 0,
f(x) = x*x/3 dla x >= 0,

– gdzie x = <-10;10> z krokiem 0.5. Współczynnik a podaje użytkownik.

Wykonanie zadania wymaga umieszczenia na wykresie dwóch funkcji. Wykorzystamy funkcję arange(), która zwraca listę wartości zmiennoprzecinkowych (zob. typy danych) z zakresu określonego przez dwa pierwsze argumenty i z krokiem wyznaczonym przez argument trzeci. Drugą przydatną konstrukcją będzie wyrażenie listowe uzupełnione o instrukcję warunkową, która ogranicza wartości, dla których obliczane jest podane wyrażenie.

2.2.1. Ćwiczenie 3¶

Zanim zrealizujemy zadanie przećwiczmy w konsoli Pythona następujący kod:

Terminal. Kod nr

>>> import pylab
>>> x = pylab.arange(-10, 10.5, 0.5)
>>> print(x)
>>> len(x)
>>> a = 3
>>> y1 = [i / -3 + a for i in x if i <= 0]
>>> len(y1)

Uwaga: nie zamykaj tej sesji konsoli, zaraz się nam jeszcze przyda.

W pliku pylab02.py umieszczamy poniższy kod:

Kod nr

#! /usr/bin/env python3
# -*- coding: utf-8 -*-

# ZADANIE: wykonaj wykres funkcji f(x), gdzie x = <-10;10> z krokiem 0.5
# f(x) = x/-3 + a dla x <= 0
# f(x) = x*x/3 dla x >= 0

import pylab

x = pylab.arange(-10, 10.5, 0.5)  # lista argumentów x
a = int(input("Podaj współczynnik a: "))
y1 = [i / -3 + a for i in x if i <= 0]

print(x, len(x))
print(y1, len(y1))

pylab.plot(x, y1)
pylab.title('Wykres f(x)')
pylab.grid(True)
pylab.show()

Uruchom program. Nie działa, dostajemy komunikat: ValueError: x and y must have same first dimension, czyli listy wartości x i y1 nie zawierają tyle samo elementów.

Co należy z tym zrobić? Jak wynika z warunków zadania, wartości y1 obliczane są tylko dla argumentów mniejszych od zera. Zatem trzeba ograniczyć listę x, tak aby zawierała tylko wartości z odpowiedniego przedziału. Wróćmy do konsoli Pythona:

2.2.2. Ćwiczenie 4¶

Terminal. Kod nr

>>> x
>>> x[0]
>>> x[0:5]
>>> x[:5]
>>> x[:len(y1)]
>>> len(x[:len(y1)])

Uwaga: nie zamykaj tej sesji konsoli, zaraz się nam jeszcze przyda.

Z pomocą przychodzi nam wydobywanie z listy wartości wskazywanych przez indeksy liczone od 0. Jednak prawdziwym ułatwieniem jest notacja wycinania (ang. slice), która pozwala podać pierwszy i ostatni indeks interesującego nas zakresu. Zmieniamy więc wywołanie funkcji plot():

Kod nr

pylab.plot(x[:len(y1)], y1)

Uruchom i przetestuj działanie programu.

Udało się nam zrealizować pierwszą część zadania. Spróbujmy zakodować część drugą. Dopisujemy:

Kod nr

y2 = [i**2 / 3 for i in x if i >= 0]

pylab.plot(x[:len(y1)], y1, x, y2)

Wyrażenie listowe wylicza nam drugą dziedzinę wartości. Następnie do argumentów funkcji plot() dodajemy drugą parę list. Spróbuj uruchomić program. Nie działa, znowu dostajemy komunikat: ValueError: x and y must have same first dimension. Teraz jednak wiemy już dlaczego...

2.2.3. Ćwiczenie 5¶

Przetestujmy kod w konsoli Pythona:

Terminal. Kod nr

>>> len(x)
>>> x[-10]
>>> x[-10:]
>>> len(y2)
>>> x[-len(y2):]

Jak widać, w notacji wycinania możemy używać indeksów ujemnych wskazujących elementy od końca listy. Jeżeli taki indeks umieścimy jako pierwszy przed dwukropkiem, czyli separatorem przedziału, dostaniemy resztę elementów listy.

Na koniec musimy więc zmodyfikować funkcję plot():

Kod nr

pylab.plot(x[:len(y1)], y1, x[-len(y2):], y2)

2.2.4. Ćwiczenie 6¶

Spróbuj dziedziny wartości x dla funkcji y1 i y2 wyznaczyć nie za pomocą notacji wycinkowej, ale przy użyciu wyrażeń listowych, których wynik przypisz do zmiennych x1 i x2. Użyj ich jako argumentów funkcji plot() i przetestuj program.

2.3. Ruchy Browna ¶

Napiszemy program, który symuluje ruchy Browna. Jak wiadomo są to chaotyczne ruchy cząsteczek, które będziemy mogli zwizualizować w płaszczyźnie dwuwymiarowej. Na początku przyjmujemy następujące założenia:

cząsteczka, której ruch będziemy śledzić, znajduje się w początku układu współrzędnych (0, 0);
w każdym ruchu cząsteczka przemieszcza się o stały wektor o wartości 1;
kierunek ruchu wyznaczać będziemy losując kąt z zakresu <0; 2Pi>;
współrzędne kolejnego położenia cząsteczki wyliczać będziemy ze wzorów:

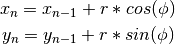
$x_n = x_{n-1} + r * cos(\phi) y_n = y_{n-1} + r * sin(\phi)$

– gdzie: r – długość jednego kroku, 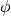$\phi$ – kąt wskazujący kierunek ruchu w odniesieniu do osi OX.

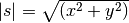
końcowy wektor przesunięcia obliczymy ze wzoru: $|s| = \sqrt{(x^2 + y^2)}$

Zacznijmy od wyliczenia współrzędnych opisujących ruch cząsteczki. Do pustego pliku o nazwie rbrowna.py wpisujemy:

Kod nr

#! /usr/bin/env python3
# -*- coding: utf-8 -*-

import numpy as np
import random

n = int(input("Ile ruchów? "))
x = y = 0

for i in range(0, n):
    # wylosuj kąt i zamień go na radiany
    rad = float(random.randint(0, 360)) * np.pi / 180
    x = x + np.cos(rad)  # wylicz współrzędną x
    y = y + np.sin(rad)  # wylicz współrzędną y
    print(x, y)

# oblicz wektor końcowego przesunięcia
s = np.sqrt(x**2 + y**2)
print("Wektor przesunięcia:", s)

Funkcje trygonometryczne zawarte w module math wymagają kąta podanego w radianach, dlatego wylosowany kąt po zamianie na liczbę zmiennoprzecinkową mnożymy przez wyrażenie math.pi / 180. Uruchom i przetestuj kod.

2.3.1. Ćwiczenie 6¶

Do przygotowania wykresu ilustrującego ruch cząsteczki generowane współrzędne musimy zapisać w listach. Wstaw w odpowiednich miejscach pliku poniższe instrukcje:

Kod nr

lx = [0]
ly = [0]

lx.append(x)
ly.append(y)

Na końcu skryptu dopisz instrukcje wyliczającą końcowy wektor przesunięcia (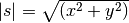 $|s| = \sqrt{(x^2 + y^2)}$ ) i drukującą go na ekranie. Przetestuj program.

Pozostaje dopisanie importu biblioteki matplotlib oraz instrukcji generujących wykres. Poniższy kod ilustruje również użycie opcji wzbogacających wykres o legendę, etykiety czy tytuł.

Kod nr

#! /usr/bin/env python3
# -*- coding: utf-8 -*-

import numpy as np
import random
import matplotlib.pyplot as plt

n = int(input("Ile ruchów? "))
x = y = 0
lx = [0]
ly = [0]

for i in range(0, n):
    # wylosuj kąt i zamień go na radiany
    rad = float(random.randint(0, 360)) * np.pi / 180
    x = x + np.cos(rad)  # wylicz współrzędną x
    y = y + np.sin(rad)  # wylicz współrzędną y
    # print(x, y)
    lx.append(x)
    ly.append(y)

print(lx, ly)

# oblicz wektor końcowego przesunięcia
s = np.fabs(np.sqrt(x**2 + y**2))
print("Wektor przesunięcia:", s)

plt.plot(lx, ly, "o:", color="green", linewidth=2, alpha=0.5)
plt.legend(["Dane x, y\nPrzemieszczenie: " + str(s)], loc="upper left")
plt.xlabel("lx")
plt.ylabel("ly")
plt.title("Ruchy Browna")
plt.grid(True)
plt.show()

Warto zwrócić uwagę na dodatkowe opcje formatujące wykres w poleceniu p.plot(lx, ly, "o:", color="green", linewidth=2, alpha=0.5). Trzeci parametr określa styl linii, możesz sprawdzić inne wartości, np: r:., r:+, r., r+. Można też określać kolor (color), grubość linii (linewidth) i przezroczystość (alpha). Poeksperymentuj.

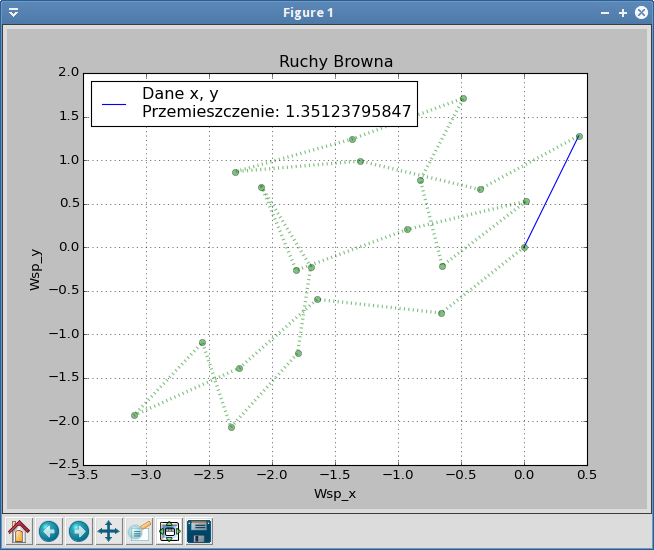
2.3.2. Ćwiczenie 7¶

Spróbuj uzupełnić kod tak, aby na wykresie zaznaczyć prostą linią w kolorze niebieskim wektor przesunięcia. Efekt końcowy może wyglądać następująco:

2.4. Zadania dodatkowe ¶

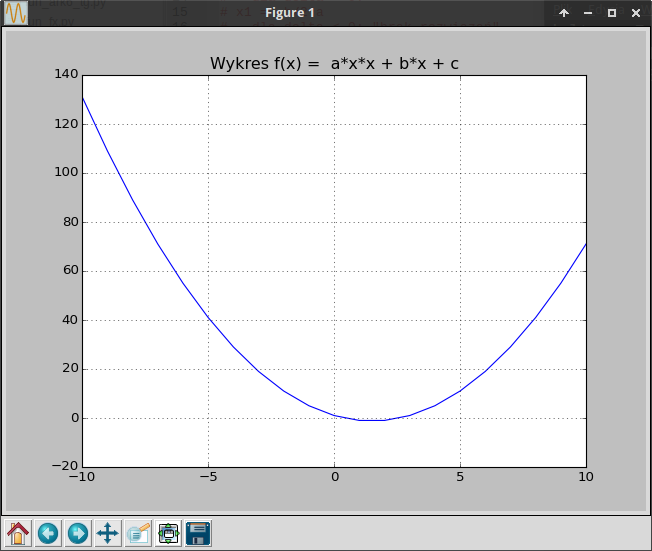
Przygotuj wykres funkcji kwadratowej: f(x) = a*x^2 + b*x + c, gdzie x = <-10;10> z krokiem 1, przyjmij następujące wartości współczynników: a = 1, b = -3, c = 1.

Uzyskany wykres powinien wyglądać następująco:

2.5. Źródła ¶

pylab.zip

Materiały Python 101 udostępniane przez Centrum Edukacji Obywatelskiej na licencji Creative Commons Uznanie autorstwa-Na tych samych warunkach 4.0 Międzynarodowa.

Utworzony:	2022-05-22 o 19:52 w Sphinx 1.5.3
Autorzy:	Patrz plik “Autorzy”

2. Matplotlib¶

2.1. Funkcja liniowa¶

2.1.1. Ćwiczenie 1¶

2.1.2. Ćwiczenie 2¶

2.2. Dwie funkcje¶

2.2.1. Ćwiczenie 3¶

2.2.2. Ćwiczenie 4¶

2.2.3. Ćwiczenie 5¶

2.2.4. Ćwiczenie 6¶

2.3. Ruchy Browna¶

2.3.1. Ćwiczenie 6¶

2.3.2. Ćwiczenie 7¶

2.4. Zadania dodatkowe¶

2.5. Źródła¶

2.1. Funkcja liniowa ¶

2.2. Dwie funkcje ¶

2.3. Ruchy Browna ¶

2.4. Zadania dodatkowe ¶

2.5. Źródła ¶