9.5. Algorytmy

W tym scenariuszu spróbujemy pokazać w Minecrafcie Pi algorytm symulujący ruchy Browna oraz algorytm stosujący metodę Monte Carlo do wyliczenia przybliżonej wartości liczby Pi.

9.5.1. Ruchy Browna

Za pomocą wybranego edytora utwórz pusty plik, umieść w nim podany niżej kod i zapisz w katalogu mcpi-sim pod nazwą mcpi-rbrowna.py:

Kod nr

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import os
import numpy as np  # import biblioteki do obliczeń naukowych
import matplotlib.pyplot as plt  # import biblioteki do tworzenia wykresow
from random import randint
from time import sleep
import mcpi.minecraft as minecraft  # import modułu minecraft
import mcpi.block as block  # import modułu block

os.environ["USERNAME"] = "Steve"  # wpisz dowolną nazwę użytkownika
os.environ["COMPUTERNAME"] = "mykomp"  # wpisz dowolną nazwę komputera

mc = minecraft.Minecraft.create("192.168.1.10")  # połączenie z serwerem


def plac(x, y, z, roz=10, gracz=False):
    """
    Funkcja tworzy podłoże i wypełnia sześcienny obszar od podanej pozycji,
    opcjonalnie umieszcza gracza w środku.
    Parametry: x, y, z - współrzędne pozycji początkowej,
    roz - rozmiar wypełnianej przestrzeni,
    gracz - czy umieścić gracza w środku
    Wymaga: globalnych obiektów mc i block.
    """

    podloga = block.SAND
    wypelniacz = block.AIR

    # podloga i czyszczenie
    mc.setBlocks(x, y - 1, z, x + roz, y - 1, z + roz, podloga)
    mc.setBlocks(x, y, z, x + roz, y + roz, z + roz, wypelniacz)
    # umieść gracza w środku
    if gracz:
        mc.player.setPos(x + roz / 2, y + roz / 2, z + roz / 2)


def wykres(x, y, tytul="Wykres funkcji", *extra):
    """
    Funkcja wizualizuje wykres funkcji, której argumenty zawiera lista x
    a wartości lista y i ew. dodatkowe listy w parametrze *extra
    """
    if len(extra):
        plt.plot(x, y, extra[0], extra[1])  # dwa wykresy na raz
    else:
        plt.plot(x, y, "o:", color="blue", linewidth="3", alpha=0.8)
    plt.title(tytul)
    plt.grid(True)
    plt.show()


def rysuj(x, y, z, blok=block.IRON_BLOCK):
    """
    Funkcja wizualizuje wykres funkcji, umieszczając bloki w pionie/poziomie
    w punktach wyznaczonych przez pary elementów list x, y lub x, z
    """
    czylista = True if len(y) > 1 else False
    for i in range(len(x)):
        if czylista:
            print(x[i], y[i])
            mc.setBlock(x[i], y[i], z[0], blok)
        else:
            print(x[i], z[i])
            mc.setBlock(x[i], y[0], z[i], blok)


def ruchyBrowna():

    n = int(raw_input("Ile ruchów? "))
    r = int(raw_input("Krok przesunięcia? "))

    x = y = 0
    lx = [0]  # lista odciętych
    ly = [0]  # lista rzędnych

    for i in range(0, n):
        # losujemy kąt i zamieniamy na radiany
        rad = float(randint(0, 360)) * np.pi / 180
        x = x + r * np.cos(rad)  # wylicz współrzędną x
        y = y + r * np.sin(rad)  # wylicz współrzędną y
        x = int(round(x, 2))  # zaokrągl
        y = int(round(y, 2))  # zaokrągl
        print(x, y)
        lx.append(x)
        ly.append(y)

    # oblicz wektor końcowego przesunięcia
    s = np.fabs(np.sqrt(x**2 + y**2))
    print "Wektor przesunięcia: {:.2f}".format(s)

    wykres(lx, ly, "Ruchy Browna")
    rysuj(lx, [1], ly, block.WOOL)


def main():
    mc.postToChat("Ruchy Browna")  # wysłanie komunikatu do mc
    plac(-80, -20, -80, 160)
    plac(-80, 0, -80, 160)
    ruchyBrowna()
    return 0


if __name__ == '__main__':
    main()

Większość kodu powinna być już zrozumiała. Importy bibliotek, nawiązywanie połączenia z serwerem MC Pi, funkcje plac(), wykres() i rysuj() omówione zostały w poprzednim scenariuszu Funkcje w mcpi.

W funkcji ruchyBrowna() na początku pobieramy od użytkownika ilość ruchów cząsteczki do wygenerowania oraz ich długość, co ma znaczenie podczas ich odwzorowywania w świecie MC Pi. Następnie w pętli:

• losujemy kąt wskazujący kierunek ruchu cząsteczki,
• wyliczamy współrzędne kolejnego punktu korzystając z funkcji cos() i sin() (np. x = x + r * np.cos(rad)),
• zaokrąglamy wyniki do 2 miejsc po przecinku (np. x = int(round(x, 2))) i drukujemy,
• na koniec dodajemy obliczone współrzędne do list odciętych i rzędnych (np. lx.append(x)).

Po wyjściu z pętli obliczamy długość wektora przesunięcia, korzystając z twierdzenia Pitagorasa, i drukujemy wynik z dokładnością do dwóch miejsc po przecinku (wyrażenie formatujące: {:.2f}).

Po tych operacjach pozostaje wykreślenie ruchu cząsteczki w matplotlib i wyznaczenie go w Minecrafcie.

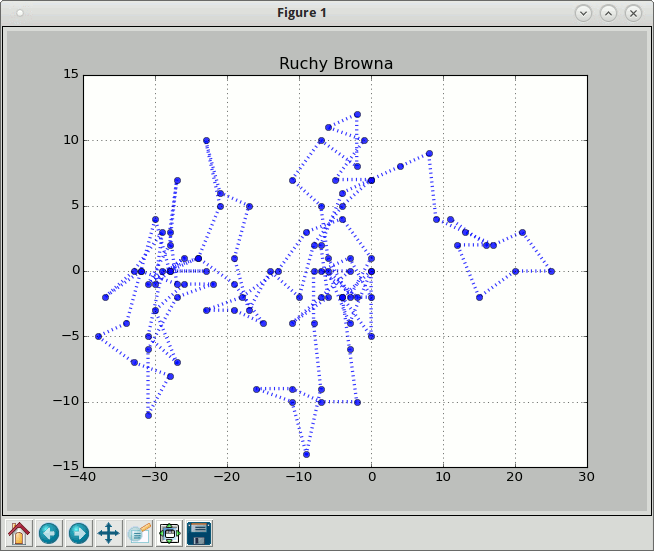
Wskazówka

Przed uruchomieniem wizualizacji warto ustawić Steve’a w tryb lotu (dwukrotne naciśnięcie spacji).

9.5.1.1. (Nie)powtarzalność

Kilkukrotne uruchomienie dotychczasowego kodu pokazuje, że za każdym razem generowany jest inny tor ruchu cząsteczki. Z jednej strony to dobrze, bo to potwierdza przypadkowość symulowanych ruchów, z drugiej strony przydatna byłaby możliwość zapamiętania wyjątkowo malowniczych sekwencji.

Zmienimy więc funkcję ruchyBrowna() tak, aby zapisywała i ewentualnie odczytywała wygenerowany i zapisany ruch cząsteczki. Musimy też dodać dwie funkcje narzędziowe zapisujące i czytające dane.

Kod nr

def ruchyBrowna(dane=[]):

    if len(dane):
        lx, ly = dane  # rozpakowanie listy
        x = lx[-1]  # ostatni element lx
        y = ly[-1]  # ostatni element ly
    else:
        n = int(raw_input("Ile ruchów? "))
        r = int(raw_input("Krok przesunięcia? "))

        x = y = 0
        lx = [0]  # lista odciętych
        ly = [0]  # lista rzędnych

        for i in range(0, n):
            # losujemy kąt i zamieniamy na radiany
            rad = float(randint(0, 360)) * np.pi / 180
            x = x + r * np.cos(rad)  # wylicz współrzędną x
            y = y + r * np.sin(rad)  # wylicz współrzędną y
            x = int(round(x, 2))  # zaokrągl
            y = int(round(y, 2))  # zaokrągl
            print(x, y)
            lx.append(x)
            ly.append(y)

    # oblicz wektor końcowego przesunięcia
    s = np.fabs(np.sqrt(x**2 + y**2))
    print "Wektor przesunięcia: {:.2f}".format(s)

    wykres(lx, ly, "Ruchy Browna")
    rysuj(lx, [1], ly, block.WOOL)
    if not len(dane):
        zapisz_dane((lx, ly))


def zapisz_dane(dane):
    """Funkcja zapisuje dane w formacie json w pliku"""
    import json
    plik = open('rbrowna.log', 'w')
    json.dump(dane, plik)
    plik.close()


def czytaj_dane():
    """Funkcja odczytuje dane w formacie json z pliku"""
    import json
    dane = []
    nazwapliku = raw_input("Podaj nazwę pliku z danymi lub naciśnij ENTER: ")
    if os.path.isfile(nazwapliku):
        with open(nazwapliku, "r") as plik:
            dane = json.load(plik)
    else:
        print "Podany plik nie istnieje!"
    return dane


def main():
    mc.postToChat("Ruchy Browna")  # wysłanie komunikatu do mc
    plac(-80, -20, -80, 160)
    plac(-80, 0, -80, 160)
    ruchyBrowna(czytaj_dane())
    return 0

Z powyższego kodu wynika, że jeżeli funkcja ruchyBrowna() otrzyma niepustą listę danych (if len(dane):), wczyta z niej dane współrzędnych x i y. W przeciwnym wypadku generowane będą nowe, które zostaną zapisane: zapisz_dane((lx, ly)).

Funkcja zapisz_dane(), pobiera tuplę zawierającą listę współrzędnych x i y, otwiera plik o podanej nazwie do zapisu (open('rbrowna.log', 'w')) i zapisuje w nim dane w formacie json.

Funkcja czytaj_dane() prosi o podanie nazwy pliku z danymi, jeśli istnieje, zwraca dane zapisane w formacie json, które w funkcji ruchyBrowna() rozpakowywane są jako listy wartości x i y: lx, ly = dane. Jeżeli podany plik z danymi nie istnieje, zwracana jest pusta lista, a w funkcji ruchyBrowna() generowane są nowe dane.

W funkcji głównej zmieniamy wywołanie funkcji na ruchyBrowna(czytaj_dane()) i testujemy zmieniony kod. Za pierwszym razem wciskamy Enter, generujemy i zapisujemy dane, za drugim razem podajemy nazwę pliku rbrowna.log.

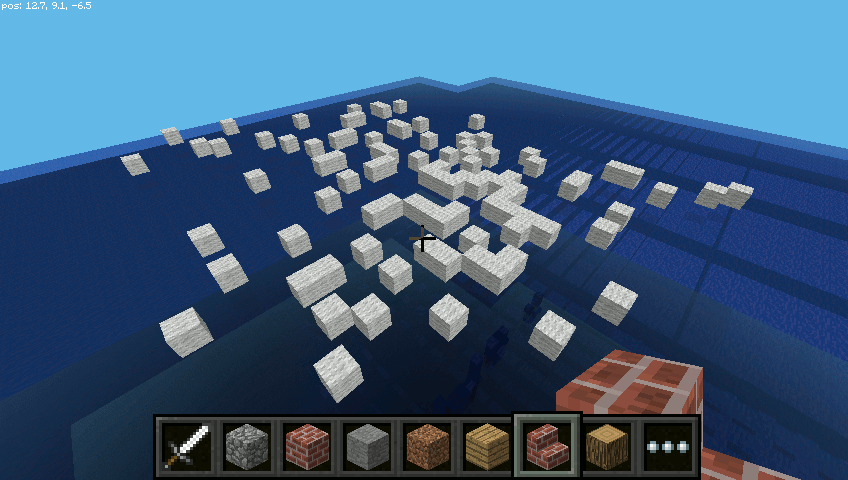
9.5.1.2. Ruch cząsteczki

Do tej pory ruch cząsteczki wizualizowane był jako pojedyncze punkty. Możemy jednak pokazać pokonaną trasę liniowo, używając omawianej już biblioteki minecraftstaff. Pod funkcją rysuj() umieszczamy następującą funkcję:

Kod nr

def rysuj_linie(x, y, z, blok=block.IRON_BLOCK):
    """
    Funkcja wizualizuje wykres funkcji, umieszczając bloki w pionie/poziomie
    w punktach wyznaczonych przez pary elementów list x, y lub x, z
    przy użyciu metody drawLine()
    """
    import local.minecraftstuff as mcstuff
    mcfig = mcstuff.MinecraftDrawing(mc)
    czylista = True if len(y) > 1 else False
    for i in range(len(x) - 1):
        x1 = int(x[i])
        x2 = int(x[i + 1])
        if czylista:
            y1 = int(y[i])
            y2 = int(y[i + 1])
            mc.setBlock(x2, y2, z[0], block.GRASS)
            mc.setBlock(x1, y1, z[0], block.GRASS)
            mcfig.drawLine(x1, y1, z[0], x2, y2, z[0], blok)
            mc.setBlock(x2, y2, z[0], block.GRASS)
            mc.setBlock(x1, y1, z[0], block.GRASS)
            print (x1, y1, z[0], x2, y2, z[0])
        else:
            z1 = int(z[i])
            z2 = int(z[i + 1])
            mc.setBlock(x1, y[0], z1, block.GRASS)
            mc.setBlock(x2, y[0], z2, block.GRASS)
            mcfig.drawLine(x1, y[0], z1, x2, y[0], z2, blok)
            mc.setBlock(x1, y[0], z1, block.GRASS)
            mc.setBlock(x2, y[0], z2, block.GRASS)
            print (x1, y[0], z1, x2, y[0], z2)
        sleep(1)  # przerwa na reklamę :-)
    mc.setBlock(0, 1, 0, block.OBSIDIAN)
    if czylista:
        mc.setBlock(x2, y2, z[0], block.OBSIDIAN)
    else:
        mc.setBlock(x2, y[0], z2, block.OBSIDIAN)

Jak widać, jest to zmodyfikowana funkcja, której użyliśmy po raz pierwszy w scenariuszu Funkcje. Zmiany dotyczą dodatkowych instrukcji typu mc.setBlock(x2, y2, z[0], block.GRASS), których zadaniem jest zaznaczenie innymi blokami wylosowanych punktów reprezentujących ruch cząsteczki. Instrukcja sleep(1) wstrzymując budowanie na 1 sekundę wywołuje wrażenie animacji i pozwala śledzić na bieżąco budowany tor. Końcowe instrukcje służą zaznaczeniu początku i końca ruchu blokami obsydianu.

Na koniec trzeba w funkcji ruchyBrowna() zmienić wywołanie rysuj() na rysuj_linie().

Eksperymenty

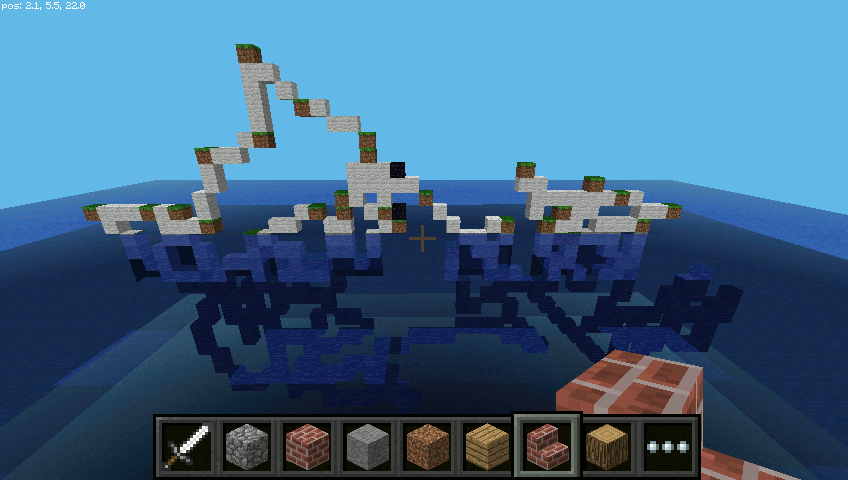
Uruchamiamy kod i eksperymentujemy. Dla 100 ruchów z krokiem przesunięcia 5 możemy uzyskać np. takie rezultaty:

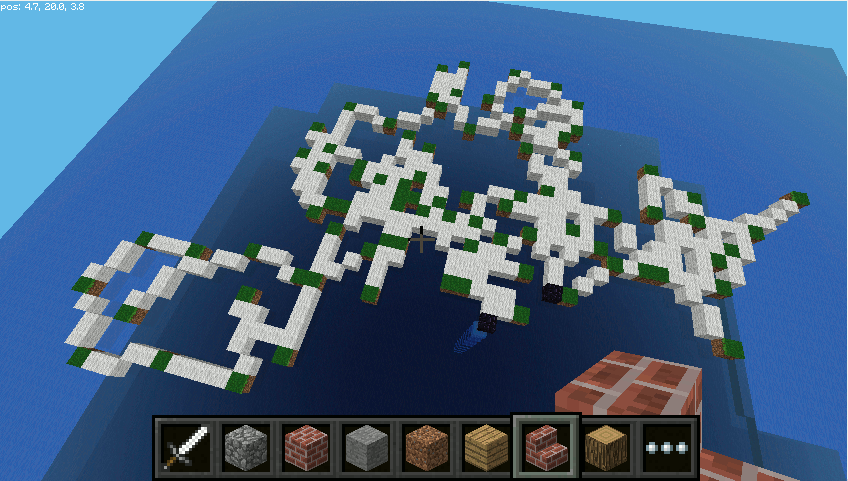
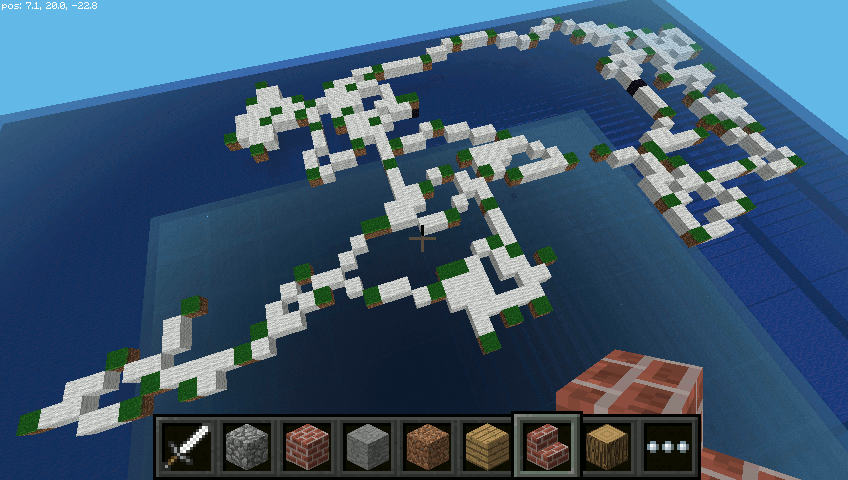
Nic nie stoina przeszkodzie, żeby cząsteczka “ruszała się” w pionie nad i... pod wodą:

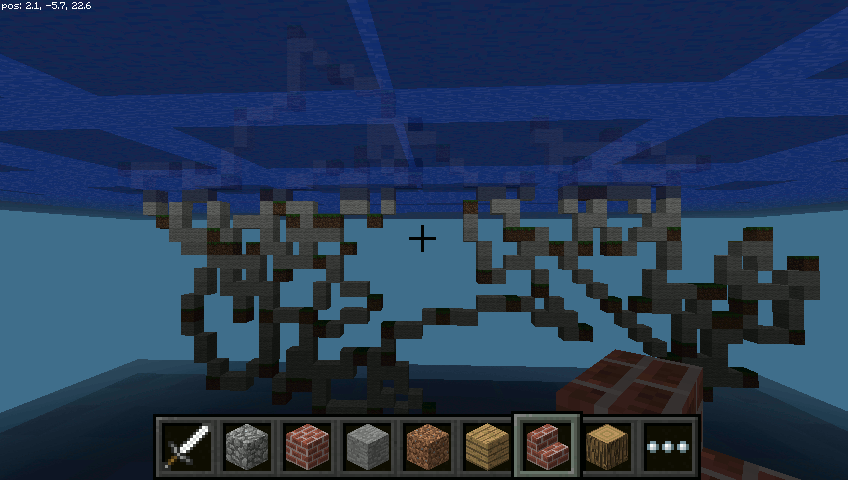
9.5.2. Liczba Pi

Mamy koło o promieniu r, którego środek umieszczamy w początku układu współrzędnych (0, 0). Na kole opisany jest kwadrat o boku 2r. Spróbujmy to zbudować w MC Pi. W pliku mcpi-lpi.py umieszczamy kod:

Kod nr

#!/usr/bin/python
# -*- coding: utf-8 -*-

import os
import random
from time import sleep
import mcpi.minecraft as minecraft  # import modułu minecraft
import mcpi.block as block  # import modułu block
import local.minecraftstuff as mcstuff

os.environ["USERNAME"] = "Steve"  # nazwa użytkownika
os.environ["COMPUTERNAME"] = "mykomp"  # nazwa komputera

mc = minecraft.Minecraft.create("192.168.1.10")  # połączenie z serwerem


def plac(x, y, z, roz=10, gracz=False):
    """Funkcja wypełnia sześcienny obszar od podanej pozycji
    powietrzem i opcjonalnie umieszcza gracza w środku.
    Parametry: x, y, z - współrzędne pozycji początkowej,
    roz - rozmiar wypełnianej przestrzeni,
    gracz - czy umieścić gracza w środku
    Wymaga: globalnych obiektów mc i block.
    """

    podloga = block.STONE
    wypelniacz = block.AIR

    # kamienna podłoże
    mc.setBlocks(x, y - 1, z, x + roz, y - 1, z + roz, podloga)
    # czyszczenie
    mc.setBlocks(x, y, z, x + roz, y + roz, z + roz, wypelniacz)
    # umieść gracza w środku
    if gracz:
        mc.player.setPos(x + roz / 2, y + roz / 2, z + roz / 2)


def model(promien, x, y, z):
    """
    Fukcja buduje obrys kwadratu, którego środek to punkt x, y, z
    oraz koło wpisane w ten kwadrat
    """

    mcfig = mcstuff.MinecraftDrawing(mc)
    obrys = block.SANDSTONE
    wypelniacz = block.AIR

    mc.setBlocks(x - promien, y, z - promien, x +
                 promien, y, z + promien, obrys)
    mc.setBlocks(x - promien + 1, y, z - promien + 1, x +
                 promien - 1, y, z + promien - 1, wypelniacz)
    mcfig.drawHorizontalCircle(0, 0, 0, promien, block.GRASS)


def liczbaPi():
    r = float(raw_input("Podaj promień koła: "))
    model(r, 0, 0, 0)


def main():
    mc.postToChat("LiczbaPi")  # wysłanie komunikatu do mc
    plac(-50, 0, -50, 100)
    mc.player.setPos(20, 20, 0)
    liczbaPi()
    return 0


if __name__ == '__main__':
    main()

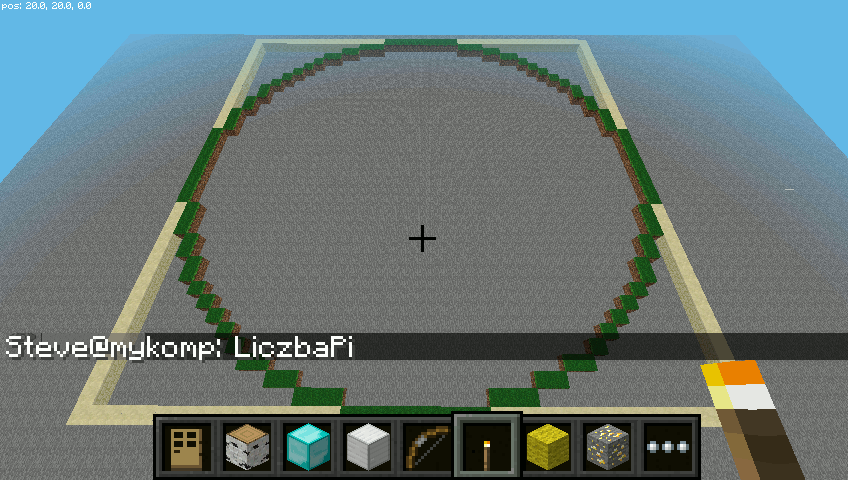
Funkcja model() działa podobnie do funkcji plac(), czyli na początku budujemy wokół środka układu współrzędnych płytę z bloku, który będzie zarysem kwadratu. Później budujemy drugą płytę o blok mniejszą z powietrza. Na koniec rysujemy koło.

9.5.2.1. Deszcz punktów

Teraz wyobraźmy sobie, że pada deszcz. Część kropel upada w obrębie kwadratu, ich ilość oznaczymy zmienną ileKw, a część również w obrębie koła – oznaczymy je zmienną ileKo. Ponieważ znamy promień koła, możemy ułożyć proporcję, zakładając, że stosunek pola koła do pola kwadratu równy będzie stosunkowi kropel w kole do kropel w kwadracie:

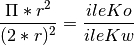
Z prostego przekształcenia tej równości możemy wyznaczyć liczbę Pi:

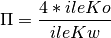
Uzupełniamy więc kod funkcji liczbaPi():

Kod nr

def liczbaPi():
    r = float(raw_input("Podaj promień koła: "))
    model(r, 0, 0, 0)

    # pobieramy ilość punktów w kwadracie
    ileKw = int(raw_input("Podaj ilość losowanych punktów: "))
    ileKo = 0  # ilość punktów w kole

    blok = block.SAND
    for i in range(ileKw):
        x = round(random.uniform(-r, r))
        y = round(random.uniform(-r, r))
        print x, y
        if abs(x)**2 + abs(y)**2 <= r**2:
            ileKo += 1
        # umieść blok w MC Pi
        mc.setBlock(x, 10, y, blok)

    mc.postToChat("W kole = " + str(ileKo) + " W Kwadracie = " + str(ileKw))
    pi = 4 * ileKo / float(ileKw)
    mc.postToChat("Pi w przyblizeniu: {:.10f}".format(pi))

Jak widać w nowym kodzie, na początku pobieramy od użytkownika ilość “kropel” deszczu, czyli punktów do wylosowania. Następnie w pętli losujemy ich współrzędne w przedziale <-r;r> w instrukcji typu: x = round(random.uniform(-r, r), 10). Funkcja uniform() zwraca wartości zmiennoprzecinkowe, które zaokrąglamy do 10 miejsca po przecinku.

Korzystając z twierdzenia Pitagorasa układamy warunek pozwalający sprawdzić, które punkty “wpadły” do koła: if abs(x)**2 + abs(y)**2 <= r**2: – i zliczamy je.

Instrukcja mc.setBlock(x, 10, y, blok) rysuje punkty w MC Pi za pomocą bloków piasku (SAND), dzięki czemu uzyskujemy efekt spadania.

Wyliczenie wartości Pi i wydrukowanie jej jest prostą formalnością.

Uruchomienie powyższego kodu dla promienia 30 i 1000 punktów dało następujący efekt:

Jak widać, niektóre punkty po zaokrągleniu ich współrzędnych w MC Pi nakładają się na siebie.

9.5.2.2. Podkolorowanie

Punkty wpadające do koła mogłyby wyglądać inaczej niż poza nim. Można by to osiągnąć przez ustawienie różnych typów bloków w pętli for, ale tylko blok piaskowy daje efekt spadania. Zrobimy więc inaczej. Zmieniamy funkcję liczbaPi():

Kod nr

def liczbaPi():
    r = float(raw_input("Podaj promień koła: "))
    model(r, 0, 0, 0)

    # pobieramy ilość punktów w kwadracie
    ileKw = int(raw_input("Podaj ilość losowanych punktów: "))
    ileKo = 0  # ilość punktów w kole
    wKwadrat = []  # pomocnicza lista punktów w kwadracie
    wKolo = []  # pomocnicza lista punktów w kole

    blok = block.SAND
    for i in range(ileKw):
        x = round(random.uniform(-r, r))
        y = round(random.uniform(-r, r))
        wKwadrat.append((x, y))
        print x, y
        if abs(x)**2 + abs(y)**2 <= r**2:
            ileKo += 1
            wKolo.append((x, y))

        mc.setBlock(x, 10, y, blok)

    sleep(5)
    for pkt in set(wKwadrat) - set(wKolo):
        x, y = pkt
        mc.setBlock(x, i, y, block.OBSIDIAN)
        for i in range(1, 3):
            print x, i, y
            if mc.getBlock(x, i, y) == 12:
                mc.setBlock(x, i, y, block.OBSIDIAN)

    mc.postToChat("W kole = " + str(ileKo) + " W Kwadracie = " + str(ileKw))
    pi = 4 * ileKo / float(ileKw)
    mc.postToChat("Pi w przyblizeniu: {:.10f}".format(pi))

Deklarujemy dwie pomocnicze listy, do których zapisujemy w pętli współrzędne punktów należących do kwadratu i koła, np. wKwadrat.append((x, y)). Następnie wstrzymujemy wykonanie kodu na 5 sekund, aby bloki piasku zdążyły opaść. W wyrażeniu set(wKwadrat) - set(wKolo) każda lista zostaje przekształcona na zbiór, a następnie zostaje obliczona ich różnica. W efekcie otrzymujemy współrzędne punktów należących do kwadratu, ale nie do koła. Ponieważ niektóre bloki piasku układają się jeden na drugim, wychwytujemy je w pętli wewnętrznej if mc.getBlock(x, i, y) == 12: – i zmieniamy na obsydian.

9.5.2.3. Trzeci wymiar

Siła MC Pi tkwi w 3 wymiarze. Możemy bez większych problemów go wykorzystać. Na początku warto zauważyć, że w algorytmie wyliczania wartości liczby Pi nic się nie zmieni. Stosunek pola koła do pola kwadratu zastępujemy bowiem stosunkiem objętości walca, którego podstawa ma promień r, do objętości sześcianu o boku 2r. Otrzymamy zatem:

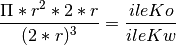
Po przekształceniu skończymy na takim samym jak wcześniej wzorze, czyli:

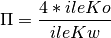
Aby to wykreślić, zmienimy funkcje model(), liczbaPi() i main(). Sugerujemy, żeby dotychczasowy plik zapisać pod inną nazwą, np. mcpi-lpi3D.py, i wprowadzić następujące zmiany:

Kod nr

def model(r, x, y, z, klatka=False):
    """
    Fukcja buduje obrys kwadratu, którego środek to punkt x, y, z
    oraz koło wpisane w ten kwadrat
    """

    mcfig = mcstuff.MinecraftDrawing(mc)
    obrys = block.OBSIDIAN
    wypelniacz = block.AIR

    mc.setBlocks(x - r - 10, y - r, z - r - 10, x +
                 r + 10, y + r, z + r + 10, wypelniacz)
    mcfig.drawLine(x + r, y + r, z + r, x - r, y + r, z + r, obrys)
    mcfig.drawLine(x - r, y + r, z + r, x - r, y + r, z - r, obrys)
    mcfig.drawLine(x - r, y + r, z - r, x + r, y + r, z - r, obrys)
    mcfig.drawLine(x + r, y + r, z - r, x + r, y + r, z + r, obrys)

    mcfig.drawLine(x + r, y - r, z + r, x - r, y - r, z + r, obrys)
    mcfig.drawLine(x - r, y - r, z + r, x - r, y - r, z - r, obrys)
    mcfig.drawLine(x - r, y - r, z - r, x + r, y - r, z - r, obrys)
    mcfig.drawLine(x + r, y - r, z - r, x + r, y - r, z + r, obrys)

    mcfig.drawLine(x + r, y + r, z + r, x + r, y - r, z + r, obrys)
    mcfig.drawLine(x - r, y + r, z + r, x - r, y - r, z + r, obrys)
    mcfig.drawLine(x - r, y + r, z - r, x - r, y - r, z - r, obrys)
    mcfig.drawLine(x + r, y + r, z - r, x + r, y - r, z - r, obrys)

    mc.player.setPos(x + r, y + r + 1, z + r)

    if klatka:
        mc.setBlocks(x - r, y - r, z - r, x + r, y + r, z + r, block.GLASS)
        mc.setBlocks(x - r + 1, y - r + 1, z - r + 1, x +
                     r - 1, y + r - 1, z + r - 1, wypelniacz)
        mc.player.setPos(0, 0, 0)

    for i in range(-r, r + 1, 5):
        mcfig.drawHorizontalCircle(0, i, 0, r, block.GRASS)


def liczbaPi(klatka=False):
    r = int(raw_input("Podaj promień koła: "))
    model(r, 0, 0, 0, klatka)

    # pobieramy ilość punktów w kwadracie
    ileKw = int(raw_input("Podaj ilość losowanych punktów: "))
    ileKo = 0  # ilość punktów w kole
    wKwadrat = []  # pomocnicza lista punktów w kwadracie
    wKolo = []  # pomocnicza lista punktów w kole

    for i in range(ileKw):
        blok = block.OBSIDIAN
        x = round(random.uniform(-r, r))
        y = round(random.uniform(-r, r))
        z = round(random.uniform(-r, r))
        wKwadrat.append((x, y, z))
        print x, y, z
        if abs(x)**2 + abs(z)**2 <= r**2:
            blok = block.DIAMOND_BLOCK
            ileKo += 1
            wKolo.append((x, y, z))

        mc.setBlock(x, y, z, blok)

    mc.postToChat("W kole = " + str(ileKo) + " W Kwadracie = " + str(ileKw))
    pi = 4 * ileKo / float(ileKw)
    mc.postToChat("Pi w przyblizeniu: {:.10f}".format(pi))
    mc.postToChat("Stan na kamieniu!")

    while True:
        poz = mc.player.getPos()
        x, y, z = poz
        if mc.getBlock(x, y - 1, z) == block.STONE.id:
            for pkt in wKolo:
                x, y, z = pkt
                mc.setBlock(x, y, z, block.SAND)
            sleep(3)
            mc.player.setPos(0, r - 1, 0)
            break


def main():
    mc.postToChat("LiczbaPi")  # wysłanie komunikatu do mc
    plac(-50, 0, -50, 100)
    liczbaPi(False)
    return 0

Zadaniem funkcji model() jest stworzenie przestrzeni dla obrysu sześcianu i jego szkieletu. Opcjonalnie, jeżeli przekażemy do funkcji parametr klatka równy True, ściany mogą zostać wypełnione szkłem. Walec wizualizujemy w pętli for rysując kilka okręgów blokami trawy.

W funkcji liczbaPi() najważniejszą zmianą jest dodanie trzeciej zmiennej. Wartości wszystkich trzech współrzędnych losowane są w takim samym zakresie, ponieważ za środek całego układu przyjmujemy początek układu współrzędnych. Ważna zmiana zachodzi w funkcji warunkowej: if abs(x)**2 + abs(z)**2 <= r**2:. Do sprawdzenia, czy punkt należy do koła wykorzystujemy zmienne x i z, uwzględniając fakt, że w MC Pi wyznaczają one położenie w poziomie.

Bloki należące do sześcianu rysujemy za pomocą obsydianu, te w walcu – za pomocą diamentów.

Na końcu funkcji dodajemy nieskończoną pętlę (while True:), której zadaniem jest sprawdzanie, na jakim bloku znajduje się gracz: if mc.getBlock(x, y - 1, z) == block.STONE.id:. Jeżeli stanie on na kamieniu, wszystkie bloki należące do walca zamieniamy w pętli for pkt in wKolo: w piasek, a gracza teleportujemy do środka sześcianu.

Dla promienia o wielkości 20 i 1000 bloków uzyskać można poniższe budowle:

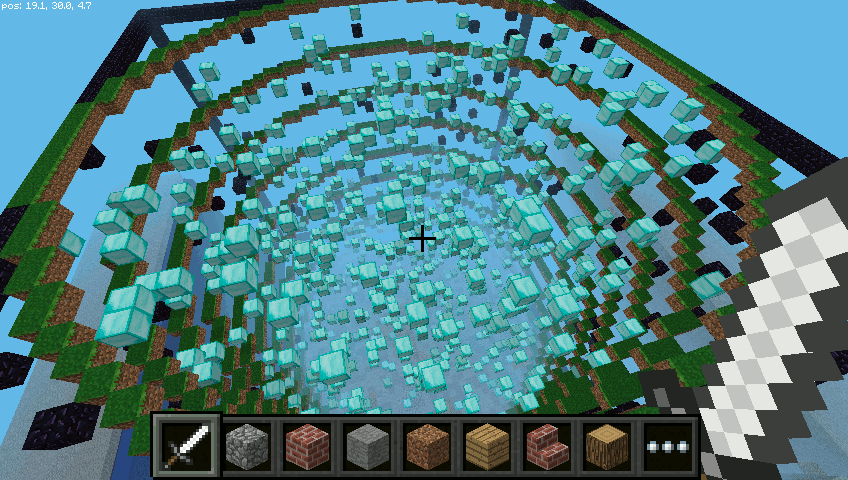
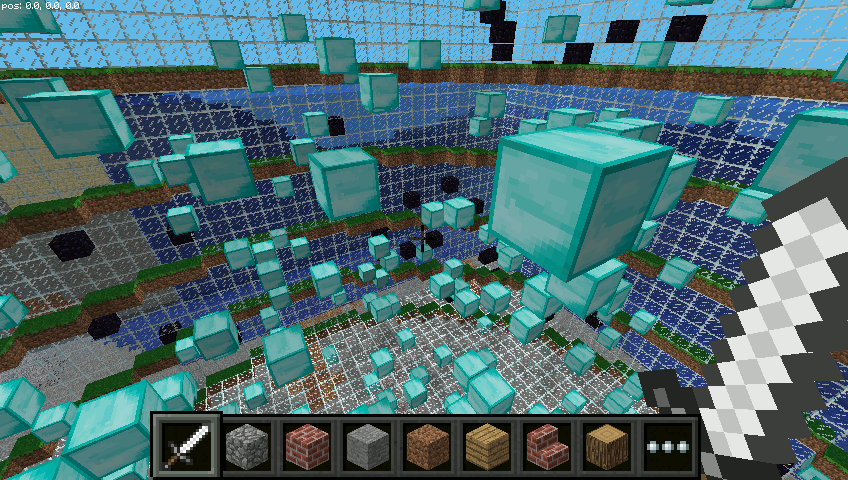
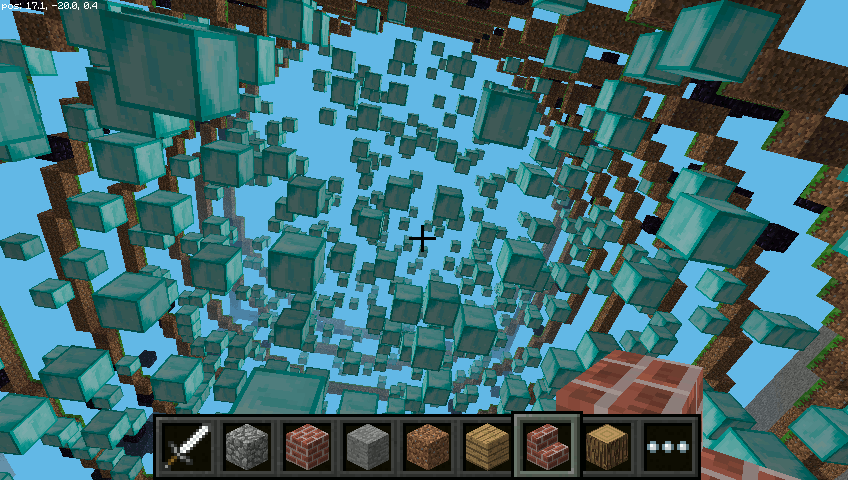
Pozostaje eksperymentować z rozmiarami, typami bloków czy parametrem klatka określanym w wywołaniu funkcji liczbaPi() w funkcji głównej.

Źródła:

• Skrypty mcpi-algorytmy

---

Materiały Python 101 udostępniane przez Centrum Edukacji Obywatelskiej na licencji Creative Commons Uznanie autorstwa-Na tych samych warunkach 4.0 Międzynarodowa.

Utworzony:2022-05-22 o 19:52 w Sphinx 1.5.3 Autorzy:Patrz plik “Autorzy”